Clinching a playoff spot: What is PPM's 95 point NHL equivalent?

In the NHL, 95 points is the magic number. More often than not, 95 points gets you into the playoffs. But what about PPM? What is PPM’s playoff threshold? I dug into Canada I.1 hockey’s records to find out for myself.
Before I get started, I need to point something obvious out. The numbers you’ll see here are for active leagues. Leagues with lots of autopilot teams and/or dead times will have much different numbers given the amount of “easy” games. If you are in a league where most people are active and almost all teams have a manager, the numbers likely will be relevant to your league as well.
I looked at the point distribution among the 20 teams from season 1 through season 19. For season’s 1-6, I re-normalized to 1140 total points since prior to season 7 ties were allowed which resulted in less than 3 points per game being handed out.
Let’s look at some data now. The plot below shows the point tally of teams ranked 1st, 9th, 11th and 16th over the 19 seasons. You can see the gap widening between 9th and 11th as well as 9th and 16th; we’ll get back to that later.
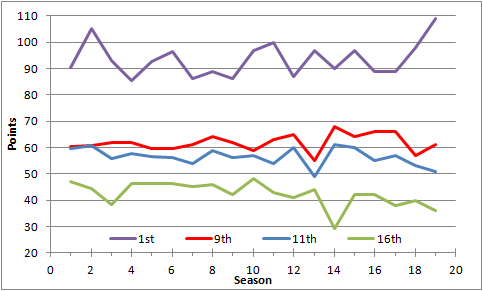
Over the course of 19 seasons, the amount of points the winning team had fluctuated greatly varying from as few as 86 to as many as 109; the average was 93.5 points. However, you don’t need 109 points to win the league; you just need more than 2nd place. Looking at second, the maximum was 99 points and the minimum was 80 points; the average was 86.5. You may be inclined to say, "well then, 87 points should, on average, take the title". And, you would be right. In 11 of 19 seasons 87 points was more than the second-place team had. But, we can be more “sure” than ~50% of the time.
In science when dealing with uncertainty, errors are quoted in terms of sigma, or standard deviations. One sigma, or one standard deviation, corresponds to the range that encloses 68.2% of data points assuming a normal (Gaussian) distribution. More commonly quoted are two sigma uncertainties. If you state a number with two sigma uncertainty, you’re saying with 95% confidence the value lies within that range. Two sigma is typically standard.
So, what is the 95% confidence level on various rankings in the league standings?
Say we want to know, with 95% confidence, how many points are required to win Canada I.1. We’d need to find the point total that lies above the 2nd place average plus 2 sigma. That is, find the point total above the 2nd-place average + ~47.5% of the points above that average. In the plot below, the point average (blue dashed line) is straddled by the max and min values (red solid line). The grey dashed line corresponds to the 95% confidence level for each league position. That is, how many points you need to earn at least that position in 19 of 20 seasons.
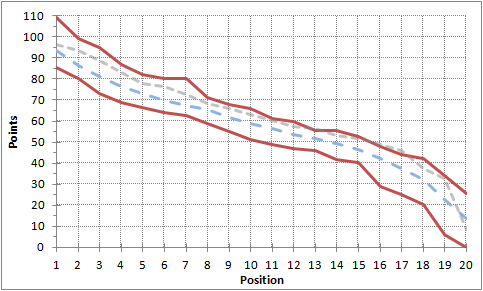
It turns out, if you want to win the title, you should be aiming for 96 points. And, when looking back at I.1 data, 96 points would have won the league 18 of 19 times (94.7%) and is on pace to win the league again this year in season 20.
Now, what about the NHL equivalent? What does it take to clinch a playoff spot in Canada I.1? Well, the 95% confidence value for 8th is 68 points. And, sure enough, 18 of 19 times 68 points was more than 9th and the other time it was equal to 9th.
The “95 point rule” in the NHL is a pretty good rule of thumb. However, this year the Bruins (96) and Kings (95) both missed the playoffs despite reaching that mark. And, just like the NHL, these 95% confidence values are just that, values that are guidelines for a specific league but are by no means guarantees. To get a “guarantee” you should use three sigma which is 99.8% confident. In the case of this dataset a 99.8% confident playoff point tally is 71.
The last comment I wanted to make was on competitiveness. Consider the plot below which shows the relationship between 9th and 1st (red) and 13th and 7th (blue). The plot shows the point difference between the two positions in terms of the point tally of the lower team. For example, a reading of 0.5 means the lower team would require 50% more points to have the same point tally as the higher team. I am using this as a proxy to judge competitiveness. Though not ideal, it is something to chew on.

At first glance it looks bad. The blue fit line rises steeply from roughly 0.25 in season 1 to 0.38 in season 19. That means the separation between 13th (mid pack) and 7th (playoff bound) is growing. There’s a catch though. Statistically, the correlation is non-existent and the relationship can simply be attributed to statistical noise, largely due to season 3 when 13th finished quite poor and 7th finished quite strong. So, I'll wait another season or two and check back.
The red data corresponds to the difference between not making the playoffs and finishing first. While scattered, the linear trend is quite low with roughly 5% gain over 19 seasons. However, statistically, this data is quite reliable having an R2 of 0.78.
“Enough nerd speak! What does it mean!?” Alright, I’m sorry, I’ll break it down a bit further. Here’s the main point on the last graph: the top clubs are still pulling away from the middle of the pack, albeit slowly. However, the level of competitiveness does not appear to be dropping as the mid-level teams continue to be healthy and consistent. This likely is attributed to the abundance of quality veteran players available on the market for cheap for younger teams.
In conclusion, just some information I wanted to share. Keep in mind it could be very different for your league be it less active or if it has one powerhouse team that goes 38-0 every season. But, if your league has a healthy point distribution and cycles through league winners, it is a good gauge to compare to the NHL. Good luck!
The Impact of Attribute Caps in Soccer
Roster Management: Quantizing Cost of Developing Players
A Systematic Collection of Career Longevity and Age Data
PPM Basketball: Tips and Advice
Balancing Money, Experience and Skill
Get PPM score updates in your email or on your phone!
Soccer Draft: Why are there more Cs and Ds than the Playboy Mansion?
PPM Basketball: Opening Thoughts
PPM Draft: Rome Wasn't Built in a Day
Chemistry and Experience: The X-Factors
PPM Hockey: The Best Defence is a Good Defence, The Best Offence is a Good Offence
Managing Your Finances - A Principled Guide to Building a Successful Hockey Team
Training Shooting: An Exercise not in Futility
Player Growth: Balancing Initial OR and EQ
Sports Academy Investigation - Article 3: SA Level and Star Players
Sports Academy Investigation - Article 2: Player PRS and SA Level Impact on Player OR
Sports Academy Investigation - Article 1: Player C/L Paths
Season 1 Training Camps: Friend or Foe?
Sports Academies: A first look at player pulls
PPM Scheduling: How teams travel from game to game
Staff: What are the most efficient ratings for my facility?
Kongsi di Facebook Kongsi di Twitter Kongsi di MySpace

 Log keluar
Log keluar